회귀분석 ③
53. 회귀분석 ③
52. 회귀분석 ② 우리는 앞에서 최소자승법에 의한 회귀계수 추정을 하면서 독립변수 x와 종속변수 Y의 관계는 선형이며, 오차항은 정규분포를 따르고, 오차항의 분산은 동일한 값을 가질 뿐만 아니라 오차항은 서..
datascream.co.kr
자료가 회귀분석에 산정하는 가정에 부합하는지 여부를 검토하는 방법을 알아보았으므로 이제는 자료가 가정을 만족시키지 못할 경우 필요한 조치에 대해 살펴보도록 하겠습니다.
오차항의 가정에서 오차항의 분산은 일정한 값을 가져야 하는데 독립변수의 값이 증가하거나 감소함에 따라 분산이 달라지는 현상이 발생할 수 있습니다.
이를 이분산성(heteroscedasticity)이라고 하는데 이분산성이 문제 될 때 최소자승추정법으로 회귀계수를 추정하게 되면 회귀계수의 표준편차가 필요 이상으로 증가하여 정확한 회귀계수의 추정이 불가능해집니다.
이분산성 문제를 제거하는 방법은 변수를 변환하는 것입니다. 만약 오차항이 독립변수와 비례관계에 있다면 이를 모형에 반영해 새로운 변수에 대한 회귀분석을 실시할 수 있습니다. 오차항 ε=kx의 관계가 성립한다면 원래의 회귀모형을 독립변수 x로 나누어 준 후 회귀분석을 실시하여 이분산성의 문제를 해결할 수 있습니다. 다만, 원래의 변수는 논리적 추론을 통해 얻은 변수인데 이를 변환하여 얻은 새로운 변수의 의미는 무엇인가라는 해석의 문제는 남게 될 것입니다.
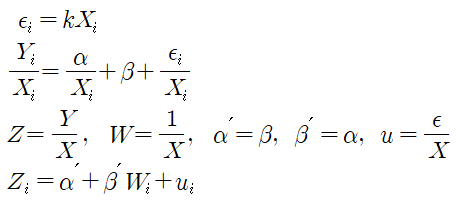
회귀분석에서 오차항이 확률적으로 독립이라는 가정이 성립하지 않는 경우로 관측값이 선행 관측값들과 상관관계를 가지는 자기상관(autocorrelation)도 있습니다.

자기상관 현상이 있으면 최소자승추정법을 적용할 경우 결정계수 R2값이 실제 이상으로 높아지고 추정 회귀분석모형이 통계적 검정을 통해 부당하게 정당화될 수도 있습니다. 독립변수 x와 종속변수 Y의 관계는 미미함에도 불구하고 단순히 오차항의 자기상관현상에 의해 회귀모형이 유의미한 것으로 잘못 판단할 수 있는 것입니다. 자기상관 역시 변수변환을 통해 제거할 수 있습니다. 이분산성의 제거와 마찬가지로 새로운 변수의 의미는 무엇인지에 대한 고민은 남게 됩니다.

이제 단순선형회귀분석에서 독립변수의 수를 추가하여 다중선형회귀분석(multiple linear regression analysis)으로 논의를 확장해 보도록 하겠습니다. 독립변수가 2개 이상이라는 점을 제외하면 적용하는 가정은 동일합니다.

① 오차항 ℇ의 평균은 0이고 ② 분산은 σ2이며 ③ 서로 확률적으로 독립이고 동일한 정규분포를 따른다. 또한 ④ 독립변수 Xi는 비확률변수입니다. 반면, 오차항 ℇ는 확률변수이고 그 결과 종속변수 Yi 역시 확률변수가 됩니다.
다중선형회귀분석에서는 독립변수가 하나가 아니므로 어떤 변수들 취사선택할 것인지가 문제됩니다. 회귀분석에 포함할 독립변수는 종속변수와 상관관계가 높으면서도 선택한 독립변수들 상호간에는 상관관계가 낮아야 할 것입니다. 다중회귀분석에서 독립변수를 선택하는 방법에는 여러 개의 독립변수 중 에서 가장 중요한 변수 순으로 하나씩 선택해 나가는 전진선택(forward selection), 전체 독립변수 중에서 불필요한 변수를 하나씩 제거하는 후진제거(backward elimination)의 방법이 있습니다. 단계적 선택(stepwise selection)은 먼저 전진선택법으로 변수를 하나씩 선택해 나가고 이미 선택한 변수에 대해서는 다중공선성이 높게 나타나는 변수를 후진제거법으로 제거해나가는 방법입니다. 다중공선성이란 세 개 이상의 독립변수들간의 강한 선형관계를 보이는 현상을 말합니다.
선행조사의 결과와 방문고객 및 담당직원과의 인터뷰 등을 종합해 볼 때 단순선형회귀분석에서 생각했던 체험형 유통점에 대한 재방문의향에 영향을 미치는 요인은 대략 다음과 같은 10가지 정도인 것이 밝혀졌다고 가정해 보겠습니다. 이들 10가지 독립변수와 종속변수인 재방문의향의 관계를 다중선형회귀분석을 이용해 알아보겠습니다.
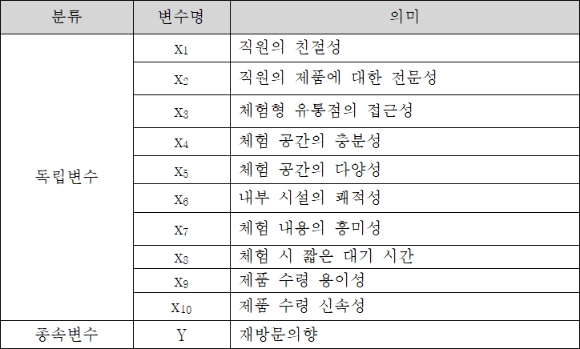
가상의 자료를 이용해 위 10개의 독립변수에 대해 다중선형회귀분석을 실시하고 단계적 선택법(stepwise selection)을 적용하여 독립변수를 선택해 보겠습니다.

선택된 독립변수들은 X1, X2, X4, X5, X7, X8의 여섯 개 변수들이고 이들 여섯 개 변수들을 대상으로 회귀계수에 대한 t검정을 실시해 본 결과 상대적으로 회귀계수의 추정치가 작은 값을 가지는 X2의 회귀계수가 통계적으로 유의미하지 않은 것으로 나타났습니다.

이제 X2를 제외하고 X1, X4, X5, X7, X8 만으로 회귀분석을 실시한 후 원래의 여섯 개 독립변수를 이용한 회귀분석과 비교해 보았습니다. X2를 제외한 회귀모형과 원래의 모형 사이에 설명력의 차이가 유의미하지 않은 것으로 보이므로 X1, X4, X5, X7, X8 을 최종 선택했습니다.

다중회귀분석에서는 이분산성이나 자기상관의 문제 외에도 세 개 이상의 독립변수들 간의 강한 선형관계를 보이는 다중공선성(multicollinearity)에 대해서도 유념해야 합니다. 특히 설문지를 이용한 횡단면 조사인 경우 여러 문항간의 다중공선성은 다소 불가피한 측면이 있습니다. 다중공선성은 회귀계수의 계산을 불가능하게 만들거나 회귀계수의 표준편차를 크게 증가시켜 정확한 통계적 검정을 할 수 없게 만들어 특정 독립변수의 독자적인 효과를 측정하는 것을 불가능하게 만듭니다.
일반적으로 독립변수간의 상관관계가 독립변수와 종속변수와의 상관관계보다 높은 경우 다중공선성을 의심해 볼 수 있습니다. 또한, 회귀계수의 표준편차가 매우 큰 값을 가지거나 회귀계수의 부호가 이론적으로 예측한 것과 반대로 나타난 경우에도 다중공선성이 의심됩니다. 독립변수를 추가하거나 삭제했을 때 혹은 자료의 미세한 변화에도 회귀계수 값의 변화가 클 경우 다중공선성을 의심할 수 있습니다.
다중공선성이 의심되는 경우에는 자료를 보완하거나 단계적 선택법을 통해 다중공선성이 의심되는 변수들 중 설명력이 낮은 변수를 제거하여 다중공선성의 문제를 완화할 수 있습니다. 그 외 서로 공행하는 독립변수들을 하나의 주성분으로 묶어 종속변수를 이들 주성분들에게 회귀시키는 주성분회귀분석(principal component regression analysis) 혹은, 공선성을 보이지 않는 외래 추정값을 활용하는 등의 방법으로 다중공선성의 문제를 완화할 수 있습니다.
궁금하신 점이 있으면 아래 버튼을 클릭해 주세요. 성실하게 답변 드리겠습니다.
'야행하는 리서치' 카테고리의 다른 글
| 53. 회귀분석 ③ (0) | 2020.03.11 |
|---|---|
| 52. 회귀분석 ② (2) | 2019.05.17 |
| 51. Borich요구도와 The Locus for Focus model (0) | 2019.01.10 |
| 50. 회귀분석 ① (0) | 2018.08.06 |
| 49. AHP(Analytical Hierarchy Process)에 대한 이해 (1) | 2018.07.06 |





