우리는 앞에서 최소자승법에 의한 회귀계수 추정을 하면서 독립변수 x와 종속변수 Y의 관계는 선형이며, 오차항은 정규분포를 따르고, 오차항의 분산은 동일한 값을 가질 뿐만 아니라 오차항은 서로 확률적으로 독립임을 가정했다. 그러므로 회귀분석에서의 추정과 검정을 신뢰하기 위해서는 자료가 가정에 부합하는지를 검토할 필요가 있다.
회귀분석의 가정을 검토하기 위해 R에서 회귀분석 결과의 산점도를 그려보겠다. plot()만으로 산점도를 그릴 수도 있겠지만 par(mfrow=)를 이용해 여러 개의 산점도를 한꺼번에 보여주면 보는 사람이 한꺼번에 판단할 수 있어 편할 것 같다. c(2,2)는 산점도를 2개씩 배열하도록 레이아웃을 지정해주는 옵션이다.
> par(mfrow=c(2,2))
> plot(output)

① 첫 번째 산점도는 잔차와 회귀식으로 예측한 Y값(fitted value, )의 관계를 보여주는 차트이다. 만약 독립변수x와 종속변수 Y이 선형관계를 가지고 오차항은 평균이 0이고 분산이 일정한 값을 가진 정규분포를 따른다면 잔차항은 과 무관하게 수평의 직선에 가까운 모습을 보일 것이다.
② 두 번째 산점도는 잔차항이 정규분포를 알아보기 위한 차트로 이론적인 정규분포 값과 잔차항을 잔차의 표준편차로 나눈 값이 직선의 형태에 부합하면 오차항이 정규분포를 따른다고 볼 수 있다. 만약 명확하지 않다면 정규성 검정절차를 거쳐 확인합니다. Shapiro 정규성 검정을 실시해 본 결과, 사례에서의 잔차항은 정규분포를 따른 것으로 볼 수 있다.

③ 세 번째 산점도는 잔차항을 잔차의 표준편차로 나눈 표준화 잔차항과 회귀식으로 예측한 Y값(fitted value, )의 관계를 보여주는 차트입니다. 오차항의 분산이 동일하다는 등분산 가정이 맞다면 표준화 잔차항은 값과 무관하게 수평의 형태를 보일 것이다.
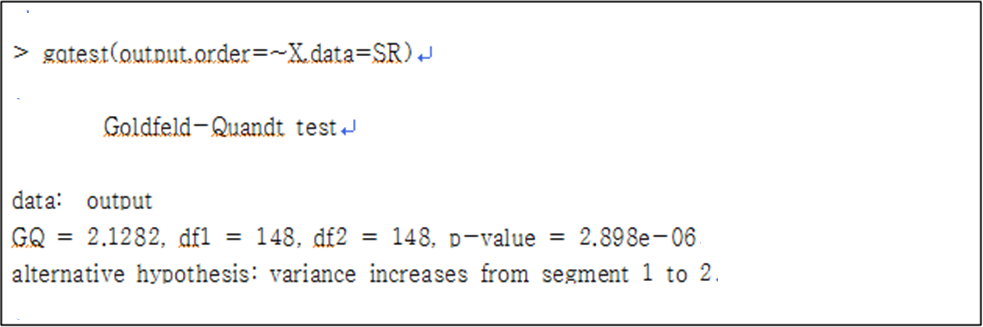
사례에서 오차항이 일정한 분산을 가진다는 등분산 가정을 좀 더 정확하게 점검하기 위해 Goldfeld-Quandt 검정을 실시해 보았다. Goldfeld-Quandt 검정은 잔차의 이분산성이 독립변수의 값과 직접 관련이 있다는 가정 하에 잔차 분산이 큰 집단과 그렇지 않은 집단을 나누어 이분산성을 검증하는 방법이다. 검정 결과 오차항의 분산은 다른지 않은 것으로 볼 수 있다. Goldfeld-Quandt 검정을 R에서 사용하기 위해서는 lmtest라는 패키지를 설치해야 하고 설치를 위해서는 관리자 권한으로 R 프로그램을 실행해야 한다.
④ 네 번째 산점도는 극단치의 존재를 확인하는 차트이다. 레버리지는 설명변수가 얼마나 치우친 값을 가지는지를 나타내는 지표이며 레버리지 값이 크다는 뜻은 극단치의 존재를 시사한다. 이는 원본 데이터의 입력이 잘못 되었거나 추가적인 데이터 수집이 필요하다는 의미이다.
회귀분석에서 오차항은 서로 확률적으로 독립이라고 가정하는데 위 네 가지 산점도로는 이를 확인할 수 없다. 오차항들의 관계를 점검하기 위해서는 별도의 검정 절차가 필요하다.
오차항의 자기 회귀 현상을 점검하기 위해 사용하는 가장 일반적인 방법으로는 Durbin-Watson 검정이 있다. Durbin-Watson 검정은 회귀분석모형에 상수항이 포함되어 있고 독립변수가 비확률변수이며 독립변수에 시차변수가 포함되지 않을 때 적용할 수 있는 검정 절차이다. Durbin-Watson 통계량은 인접한 잔차항들 간의 차이의 제곱합을 잔차의 제곱합으로 나눈 값인데 잔차들 간에 자기 회귀 현상이 없다면 Durbin-Watson 통계량은 2에 가까운 값을 갖게 된다. 사례에서 Durbin-Watson 검정을 실시한 결과 오차항들간의 자기회귀현상은 없는 것으로 판단할 수 있을 것 같다.

자료가 회귀분석에 산정하는 가정에 부합하는지 여부를 검토하는 방법을 알아보았으므로 다음 포스팅에서는 자료가 가정을 만족시키지 못할 경우 필요한 조치에 대해 살펴보고자 한다.
'야행하는 리서치' 카테고리의 다른 글
| 54. 회귀분석 ④ (0) | 2020.05.07 |
|---|---|
| 52. 회귀분석 ② (2) | 2019.05.17 |
| 51. Borich요구도와 The Locus for Focus model (0) | 2019.01.10 |
| 50. 회귀분석 ① (0) | 2018.08.06 |
| 49. AHP(Analytical Hierarchy Process)에 대한 이해 (1) | 2018.07.06 |





