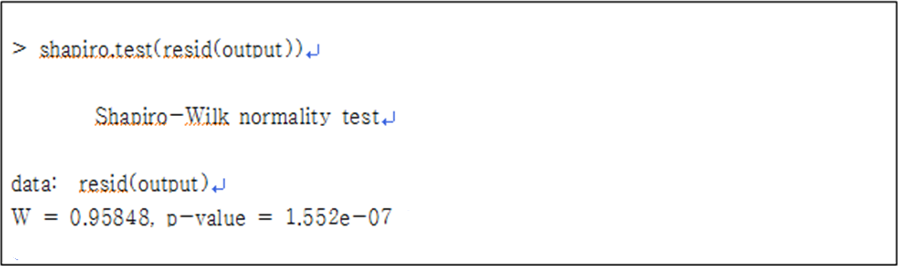
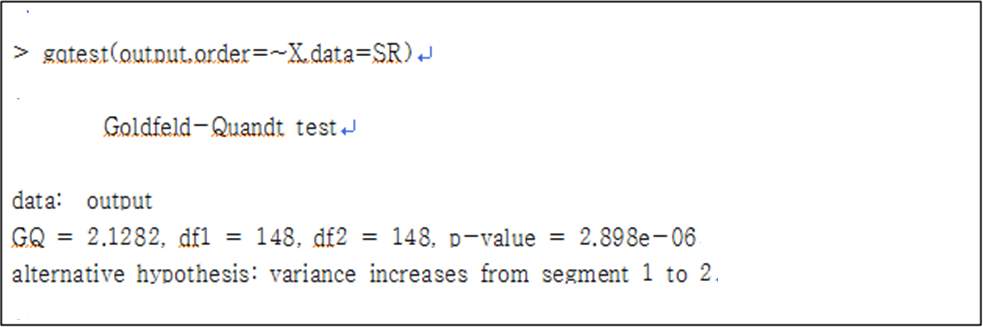
서베이몽키 Premier 계정에서는 고급 분기 기능을 제공하고 있어 좀 더 다양한 로직 적용이 가능합니다. 고급분기에 대해서는 복수응답이 가능한 확인란을 기준으로 이미 다룬 바 있습니다. 이번에는 드롭다운 메뉴 행렬에서 고급분기 로직을 적용해 보겠습니다.

33. 서베이몽키 고급분기3 보러가기

코로나19 상황 이후 동네슈퍼와 전통시장의 소상공인을 지원하기 위해 일반 소비자들을 대상으로 코로나19 상황 전후로 주요 식료품 유통채널별 이용 빈도의 변화를 점검하는 설문조사를 가정하여 고급분기로직을 적용하겠습니다. 주요 유통채널 중 동네슈퍼와 전통시장에 대해 코로나 19 상황 전에는 월 2회 이상 식료품을 구매했지만 코로나19 상황 후에는 월 1회 이하로 식료품을 구매하고 있는 소비자들에게 구매 빈도가 감소한 이유를 묻는 질문을 서베이몽키 드롭다운 메뉴 행렬과 확인란(중복응답)으로 구현해 보겠습니다.

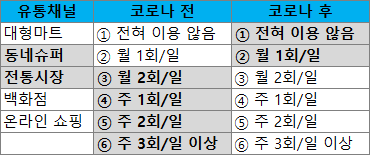
우선 드롭다운 메뉴 행렬로 설문을 구성해 보겠습니다. 드롭다운 메뉴 행렬에서 유통채널을 입력해주고 열은 코로나 전과 코로나 후를 추가해 줍니다. 다음으로 열의 보기를 입력합니다.

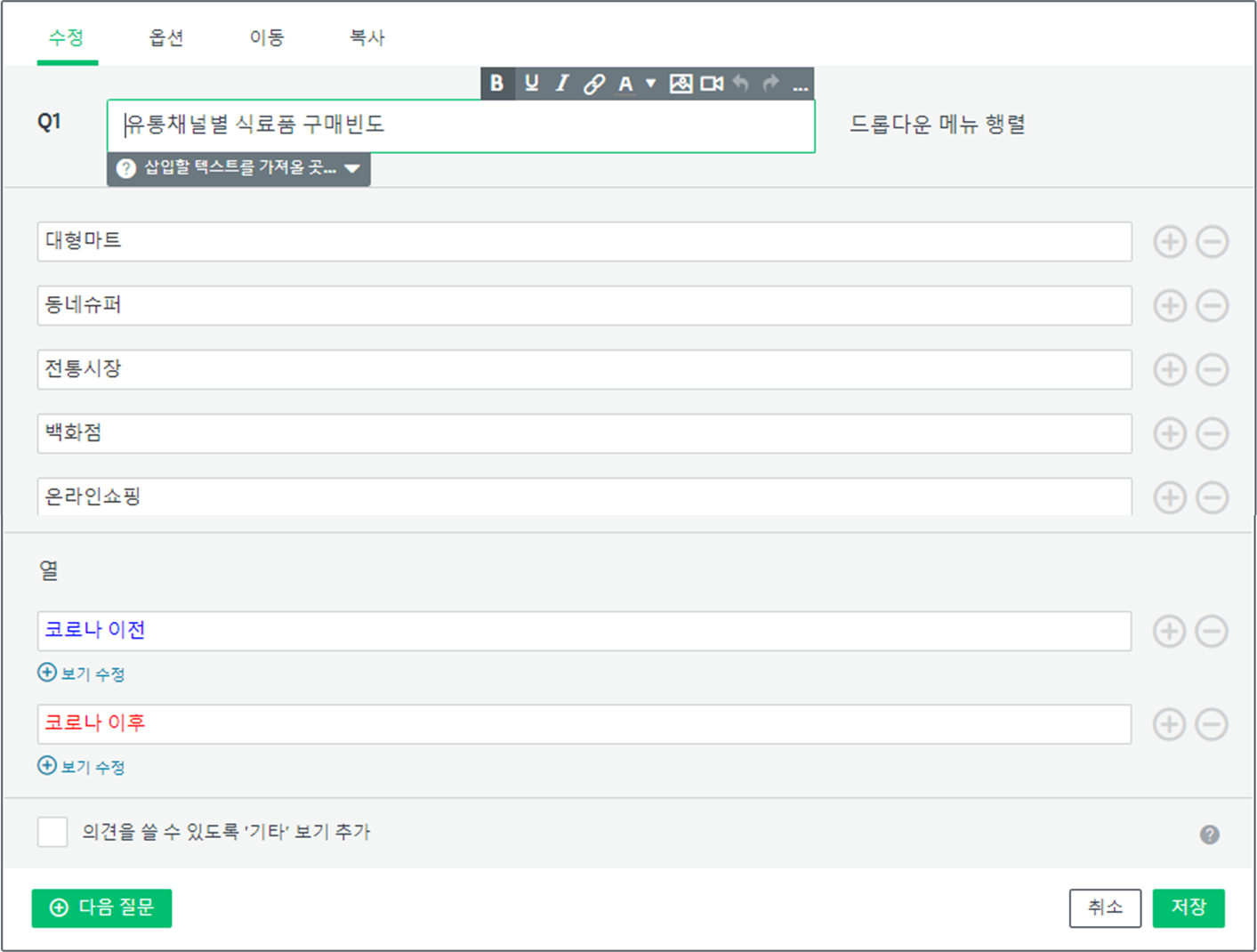
드롭다운 메뉴 행렬을 완성한 후에는 해당 페이지 상단의 페이지 로직에서 고급 분기 로직에서 원하는 규칙을 입력합니다. 동네슈퍼에 대해서 코로나 전후로 필요한 조건을 선택하고 조건을 충족할 경우 이동할 페이지도 선택해 줍니다.

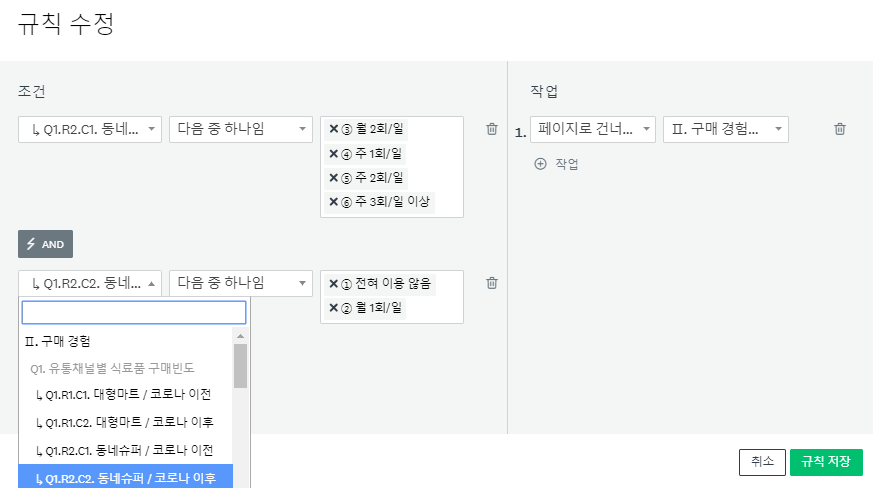
다음으로 전통시장에 대해서도 동일하게 규칙을 입력해주고 규칙 적용 후 이동할 페이지도 지정해 줍니다. 이동할 페이지의 페이지 제목에 페이지 제목 배경색과 동일한 색상으로 간략한 설명을 추가하면 응답자에게는 설명을 노춣하지 않으면서도 정확한 규칙을 입력할 수 있습니다. 복잡한 로직을 적용해야 하는 경우에는 조금 번거롭더라도 플로우 차트를 정확하게 작성한 후 규칙을 입력하는 것이 좋습니다.

서베이몽키 드롭다운 메뉴 행렬에서 구현한 고급 분기 로직은 아래 링크에서 확인해 보시기 바랍니다.

https://ko.surveymonkey.com/r/9G5FSN5

링크에서 확인해보면 동네슈퍼와 전통시장을 구분하지 않고 이용 빈도가 감소한 이유를 묻고 있습니다. 아쉽게도 드롭다운 메뉴 행렬에서 규칙을 적용하는 과정에서 상호모순인 규칙을 적용해야 할 경우가 발생했기 때문에 예시 설문에서 동네 슈퍼와 전통시장을 구분해서 이유를 묻는 방법은 찾지 못했습니다. 현재로서는 서베이몽키에서 복수의 보기 선택에 복수의 로직을 적용하는 방법으로는 해당하는 조건들에 해당하는 페이지를 하나 하나 만들어 대응시키는 것만을 찾은 상황입니다. 서베이몽키가 제공하는 기능의 범위 내에서 다른 방법이 있는지는 여전히 찾고 있는 중입니다.

궁금하신 점이 있으면 아래 버튼을 클릭해 주세요. 성실하게 답변 드리겠습니다.

대체로 신제품개발단계는 아래와 같은 절차를 거치게 됩니다.

신제품개발단계에서 아래와 같이 구매예상시기를 묻는 질문은 예비시험조사 단계의 유치조사(Home Use Test)에서 실시하는 것이 효과적이라고 생각합니다. 컨셉트 평가 단계에서 아래와 같은 질문이 의미가 있으려면 컨셉트의 정제 수준이 매우 높고 패키지나 시제품(mock-up) 등을 제시할 수 있어 응답하는 소비자가 어느 정도 구체적으로 상상할 수 있어야 합니다.

Q1. 귀하는 향후 ‘OOO’ 을(를) 구매할 계획이 있습니까?

구매할 계획이 없다 ························· 1 

6개월 이내에 구매할 계획이다 ······ 2

1개월 이내에 구매할 계획이다 ······ 3

 위의 질문은 구매 시기를 완비된 형태로 제시하지 않았기 때문에 일반적으로는 구매의향이 있는 소비자의 비율을 과소추정하게 되는 경쟁가설로 작용할 우려가 있습니다. 응답자의 입장에서 위 설문의 보기 ‘6개월 이내’나 ‘1개월 이내’는 너무 촉박한 기간일 수 있으며. 좀 더 다양한 구매예상기간이 보기로 제시되어야 합니다. 또한, 응답자 입장에서는 구매할 의향은 있지만 언제 구매할지는 아직 결정하지 못한 경우도 있으므로 이를 반영한 보기를 제시해야 합니다. 이러한 보기가 모두 반영되었을 때 컨셉트와 제품을 이루는 요소 중 소비자에게 보다 더 호소력이 있는 것은 무엇인지, 어떤 요소가 구매를 주저하게 되는 장애 요인인지 보다 명백해지기도 합니다.

신제품개발과정은 선형적으로 진행하기보다는 아래와 같이 나선형을 이루며 진행되는 것이 일반적이므로 개발과정에 맞춰 조사표의 질문 역시 그 형태와 구체화 정도를 달리해야 할 것입니다.

52. 회귀분석 ②

우리는 앞에서 최소자승법에 의한 회귀계수 추정을 하면서 독립변수 x와 종속변수 Y의 관계는 선형이며, 오차항은 정규분포를 따르고, 오차항의 분산은 동일한 값을 가질 뿐만 아니라 오차항은 서로 확률적으로 독립임을 가정했다. 그러므로 회귀분석에서의 추정과 검정을 신뢰하기 위해서는 자료가 가정에 부합하는지를 검토할 필요가 있다.

회귀분석의 가정을 검토하기 위해 R에서 회귀분석 결과의 산점도를 그려보겠다. plot()만으로 산점도를 그릴 수도 있겠지만 par(mfrow=)를 이용해 여러 개의 산점도를 한꺼번에 보여주면 보는 사람이 한꺼번에 판단할 수 있어 편할 것 같다. c(2,2)는 산점도를 2개씩 배열하도록 레이아웃을 지정해주는 옵션이다.

> par(mfrow=c(2,2))

> plot(output)

① 첫 번째 산점도는 잔차와 회귀식으로 예측한 Y값(fitted value, )의 관계를 보여주는 차트이다. 만약 독립변수x와 종속변수 Y이 선형관계를 가지고 오차항은 평균이 0이고 분산이 일정한 값을 가진 정규분포를 따른다면 잔차항은 과 무관하게 수평의 직선에 가까운 모습을 보일 것이다.

② 두 번째 산점도는 잔차항이 정규분포를 알아보기 위한 차트로 이론적인 정규분포 값과 잔차항을 잔차의 표준편차로 나눈 값이 직선의 형태에 부합하면 오차항이 정규분포를 따른다고 볼 수 있다. 만약 명확하지 않다면 정규성 검정절차를 거쳐 확인합니다. Shapiro 정규성 검정을 실시해 본 결과, 사례에서의 잔차항은 정규분포를 따른 것으로 볼 수 있다.

③ 세 번째 산점도는 잔차항을 잔차의 표준편차로 나눈 표준화 잔차항과 회귀식으로 예측한 Y값(fitted value, )의 관계를 보여주는 차트입니다. 오차항의 분산이 동일하다는 등분산 가정이 맞다면 표준화 잔차항은 값과 무관하게 수평의 형태를 보일 것이다.

사례에서 오차항이 일정한 분산을 가진다는 등분산 가정을 좀 더 정확하게 점검하기 위해 Goldfeld-Quandt 검정을 실시해 보았다. Goldfeld-Quandt 검정은 잔차의 이분산성이 독립변수의 값과 직접 관련이 있다는 가정 하에 잔차 분산이 큰 집단과 그렇지 않은 집단을 나누어 이분산성을 검증하는 방법이다. 검정 결과 오차항의 분산은 다른지 않은 것으로 볼 수 있다. Goldfeld-Quandt 검정을 R에서 사용하기 위해서는 lmtest라는 패키지를 설치해야 하고 설치를 위해서는 관리자 권한으로 R 프로그램을 실행해야 한다.

④ 네 번째 산점도는 극단치의 존재를 확인하는 차트이다. 레버리지는 설명변수가 얼마나 치우친 값을 가지는지를 나타내는 지표이며 레버리지 값이 크다는 뜻은 극단치의 존재를 시사한다. 이는 원본 데이터의 입력이 잘못 되었거나 추가적인 데이터 수집이 필요하다는 의미이다.

회귀분석에서 오차항은 서로 확률적으로 독립이라고 가정하는데 위 네 가지 산점도로는 이를 확인할 수 없다. 오차항들의 관계를 점검하기 위해서는 별도의 검정 절차가 필요하다.

오차항의 자기 회귀 현상을 점검하기 위해 사용하는 가장 일반적인 방법으로는 Durbin-Watson 검정이 있다. Durbin-Watson 검정은 회귀분석모형에 상수항이 포함되어 있고 독립변수가 비확률변수이며 독립변수에 시차변수가 포함되지 않을 때 적용할 수 있는 검정 절차이다. Durbin-Watson 통계량은 인접한 잔차항들 간의 차이의 제곱합을 잔차의 제곱합으로 나눈 값인데 잔차들 간에 자기 회귀 현상이 없다면 Durbin-Watson 통계량은 2에 가까운 값을 갖게 된다. 사례에서 Durbin-Watson 검정을 실시한 결과 오차항들간의 자기회귀현상은 없는 것으로 판단할 수 있을 것 같다.

자료가 회귀분석에 산정하는 가정에 부합하는지 여부를 검토하는 방법을 알아보았으므로 다음 포스팅에서는 자료가 가정을 만족시키지 못할 경우 필요한 조치에 대해 살펴보고자 한다.